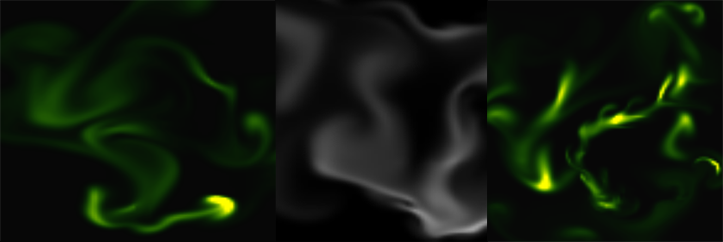
Implementing real time fluid simulation in pure Javascript was a long desire of me and has been sitting in my todo list from a long time on. However from various reasons i never found enough time to start working on it. I know it's nothing new and there are quite a few implementations done on canvas already (maybe the best known is this: http://nerget.com/fluidSim/), but i wanted to do mine without to relay to others work and to use the core logic as found on the original paper.

For me one of the most inspiring real-time 2D fluid simulations based on Navier Stokes equations was that created by Memo Akten, originally implemented in Processing (a Java based programming language, very suitable for digital artists for visual experimentation), lately ported to OpenFrameworks (a C++ framework) then implemented in AS 3.0 by Eugene Zatepyakin http://blog.inspirit.ru/?p=248.

The code is based on Jos Stam’s famous paper - Real-Time Fluid Dynamics for Games, but another useful resource which i found during preparation and development was a paper from Mike Ash: Fluid Simulation for Dummies. As the title suggest, the concept is explained very clearly even if the equations behind are quite complex, which means without a good background in physics and differential equations it's difficult to understand. This does not means that i'm a little genius in maths or physics :). In this post i will sketch briefly some of the main concepts behind the theory and more importantly how can be implemented in Javascript. As a side note, this simulation does not take advantages of the GPU power, so it's not running on WebGL. For a WebGL implementation see http://www.ibiblio.org/e-notes/webgl/gpu/fluid.htm.

The basic concept

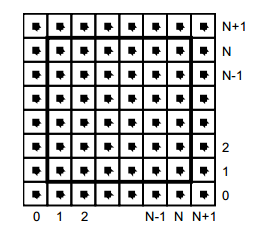
We can think of fluids as a collection of cells or boxes (in 3D), each one interacting with it's neighbor. Each cell has some basic properties like velocity and density and the transformation taking place in one cell is affecting the properties of neighbor cells (all of these happening million times per second).

Being such a complex operation, computers (even the most powerful ones) can not simulate real time the fluid dynamics. For this we need to make some compromise. We'll break the fluid up into a reasonable number of cells and try to do several interactions per second. That's what Jos Stam's approaching is doing great: sacrifice the fluid accuracy for a better visual presentation, more suitable for running real time. The best way to improve the simulation fluency is to reduce the solver iteration number. We'll talk about this a little bit later.

First we are staring by initializing some basic properties like the number of cells, the length of the timestamp, the amount of diffusion and viscosity etc. Also we need a density array and a velocity array and for each of them we set up a temporary array to switch the values between the new and old ones. This way we can store the old values while computing the new ones. Once we are done with the iteration we need to reset all the values to the default ones. For efficiency purposes we'll use single dimensional array over double ones.

The first step is to add some density to our cells:

function addDensitySource(x, x0) {                
	var size = self.numCells;        
	while(size-- > -1) {
		x[size] += _dt * x0[size];
	}
}

then to add some velocity:

FSolver.prototype.addCellVelocity = function() {
	var size = self.numCells;
	while(size-- > -1) {
		if (isNaN(self.u[size])) continue;
		self.u[size] += _dt * self.uOld[size];
		if (isNaN(self.v[size])) continue;
		self.v[size] += _dt * self.vOld[size];
	}
}

Because some of the functions needs to be accessible only from main script i separated the internal (private) functions from the external (public) functions. But because Javascript is a prototypical language i used the object prototype method to extend it. That's why some of the methods are declared with prototype and others as simple functions. However these aren't accessible from the outside of FS namespace, which is declared as a global namespace. For this technique please see this great article Learning JavaScript Design Patterns.

The process

The basic structure of our solver is as follows. We start with some initial state for the velocity and the density and then update its values according to events happening in the environment. In our prototype we let the user apply forces and add density sources with the mouse (or we can extend this to touching devices too). There are many other possibilities this can be extended.

Basically to simulate the fluid dynamics we need to familiarize our self with three main operations:

Diffusion:

Diffusion is the process when - in our case - the liquids doesn't stay still, but are spreading out. Through diffusion each cell exchanges density with its direct neighbors. The array for the density is filled in from the user's mouse movement. The cell’s density will decrease by losing density to its neighbors, but will also increase due to densities flowing in from the neighbors.

Projection:

This means the amount of fluid going in has to be exactly equal with the amount of fluid going out, otherwise may happens that the net inflow in some cells to be higher or lower than the net inflow of the neighbor cells. This may cause the simulation to react completely chaotic. This operation runs through all the cells and fixes them up to maintain in equilibrium.

Advection:

The key idea behind advection is that moving densities would be easy to solve if the density were modeled as a set of particles. In this case we would simply have to trace the particles though the velocity field. For example, we could pretend that each grid cell’s center is a particle and trace it through the velocity field. So advection in fact is a velocity applied to each grid cell. This is what makes things move.

setBoundary():

We assume that the fluid is contained in a box with solid walls: no flow should exit the walls. This simply means that the horizontal component of the velocity should be zero on the vertical walls, while the vertical component of the velocity should be zero on the horizontal walls. So in fact every velocity in the layer next to the outer layer is mirrored. The following code checks the boundaries of fluid cells.

function setBoundary(bound, x) {
	var dst1, dst2, src1, src2, i;
	var step = FLUID_IX(0, 1) - FLUID_IX(0, 0);
	dst1 = FLUID_IX(0, 1);
	src1 = FLUID_IX(1, 1);
	dst2 = FLUID_IX(_NX+1, 1);
	src2 = FLUID_IX(_NX, 1);

	if (wrap_x) {
		src1 ^= src2;
		src2 ^= src1;
		src1 ^= src2;
	}

	if (bound == 1 && !wrap_x) {
		for (i = _NY; i > 0; --i) {
			x[dst1] = -x[src1]; dst1 += step; src1 += step;
			x[dst2] = -x[src2]; dst2 += step; src2 += step;
		}
	} else {
		for (i = _NY; i > 0; --i) {
			x[dst1] = x[src1]; dst1 += step; src1 += step;
			x[dst2] = x[src2]; dst2 += step; src2 += step;
		}
	}

	dst1 = FLUID_IX(1, 0);
	src1 = FLUID_IX(1, 1);
	dst2 = FLUID_IX(1, _NY+1);
	src2 = FLUID_IX(1, _NY);

	if (wrap_y) {
		src1 ^= src2;
		src2 ^= src1;
		src1 ^= src2;
	}

	if (bound == 2 && !wrap_y) {
		for (i = _NX; i > 0 ; --i) {
			x[dst1++] = -x[src1++];
			x[dst2++] = -x[src2++];
		}
	} else {
		for (i = _NX; i > 0; --i) {
			x[dst1++] = x[src1++];
			x[dst2++] = x[src2++];
		}
	}

	x[FLUID_IX(0, 0)] = .5 * (x[FLUID_IX(1, 0)] + x[FLUID_IX(0, 1)]);
	x[FLUID_IX(0, _NY+1)] = .5 * (x[FLUID_IX(1, _NY+1)] + x[FLUID_IX(0, _NY)]);
	x[FLUID_IX(_NX+1, 0)] = .5 * (x[FLUID_IX(_NX, 0)] + x[FLUID_IX(_NX+1, _NX)]);
	x[FLUID_IX(_NX+1, _NY+1)] = .5 * (x[FLUID_IX(_NX, _NY+1)] + x[FLUID_IX(_NX+1, _NY)]);
}

The main simulation function is implemented as follow:

FSolver.prototype.updateDensity = function() {        
	addDensitySource(this.density, this.densityOld);

	if (_doVorticityConfinement) {            
		calcVorticityConfinement(this.uOld, this.vOld);            
	}

	diffuse(0, this.densityOld, this.density, 0);
	advect(0, this.density, this.densityOld, this.u, this.v);
}

FSolver.prototype.updateVelocity = function() {
	this.addCellVelocity();
	this.SWAP('uOld', 'u');
	diffuse(1, this.u, this.uOld, _visc);
	this.SWAP('vOld', 'v');        
	diffuse(2, this.v, this.vOld, _visc);        
	project(this.u, this.v, this.uOld, this.vOld);

	this.SWAP('uOld', 'u');
	this.SWAP('vOld', 'v');
	advect(1, this.u, this.uOld, this.uOld, this.vOld);
	advect(2, this.v, this.vOld, this.uOld, this.vOld);
	project(this.u, this.v, this.uOld, this.vOld);
}

We are calling these functions on each frame on the main drawing method. For rendering the cells i used canvas putImageData() method which accepts as parameter an image data, whose values are in fact the fluid solver values obtained from the density array. My first attempt was to generate a particle field, associate to each particle density, velocity etc. (so all the data necessarily making a fluid simulation), connect each particle in a single linked list, knowing this is a much faster method for constructing an array, instead using the traditional one. Then using a fast and efficient method to trace a line, best known as Extremely Fast Line Algorithm or Xiaolin Wu's line algorithm with anti aliasing (http://www.bytearray.org/?p=67) i thought i could gain more FPS for a smoother animation, but turned out being a very buggy implementation, so for the moment i abandoned the idea, but i will revised once i will have more time. Anyway i don't swipe out this code part. You can find some utility functions too for my attempting, like implementing the AS3 Bitmap and BitmapData classes.

And here is the monochrome version:
www.esimov.com/experiments/javascript/fluid-solver-mono/

The simulation is fully adapted to touch devices, but i think you need a really powerful device to run the fluid simulation decently.

What's next?

That's all. Hopefully this will be a solid base to explore further this field and add some extra functionality.